What should you do when you come up with too many numbers and to
play them all, you’d have to buy too many tickets, making the game rather expensive?
Here is when the ‘Cycles’ function steps in.
The idea behind it is based on an observation that all the numbers from the pool
(most lotteries have ~50 numbers) have to be drawn regularly.
So there is no way the number for instance, is drawn constantly every second or third draw,
and the number 15 shows up on average every 40 draws.
The range of draws, in which all numbers from the pool
were drawn is called the Cycle.
For example (lottery 6/49): when we start counting the first cycle from the draw of 1 March,
on April 18, after let's say 22 draws - all 49 numbers will be drawn (some of them more than once obviously).
From the next draw (e.g. 20th April) a second cycle starts.
This is how the cycles are calculated.
What is the most interested to us:
- in what order do the numbers show up within the cycle? (e.g. the numbers 5 and 6 often
begin a cycle or appear at the very beginning)..
- ..and more importantly: What number has not yet been drawn?
Before calculating cycles you have to define the
start draw. By default it’s the first lottery result
in the Keniox database. By changing the starting point it’s possible to
find such a cycle in
which the
number of missing numbers (that have not been drawn yet)
is minimal.
Please notice that each draw may be assigned to many cycles.
You can calculate the overall cycles’ lengths: average, min and max.
By
comparing these missing numbers with ours (chosen so far) –
the more likely numbers can be picked.
In addition there are also details available for each cycle:
numbers order, their coming-out frequency and the last date the number was drawn.
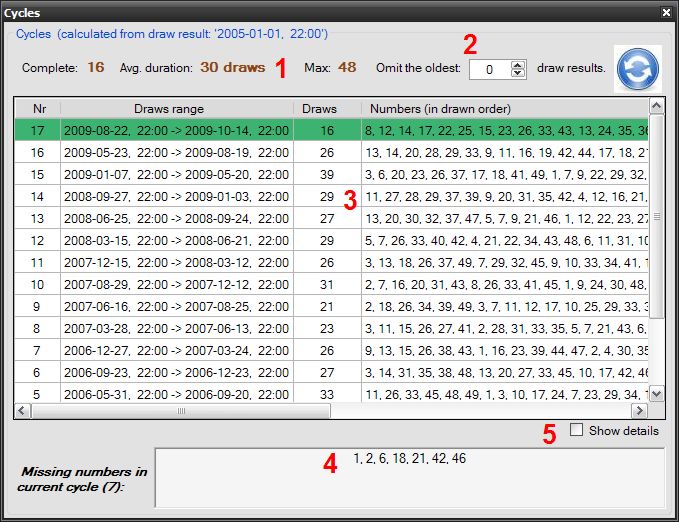
1 - Figures: the number of complete cycles, min, max and avg. cycle's length.
2 - Definition of starting point for the calculation of cycles. By default: Keniox omits 0 draw results;
it starts from first draw in the database. Increase this number to change starting date (visible on the header).
3 - Output table contains:
- "Nr" - the number of the cycle (started from the newest one)
- "Draws' range" - the beginning and the end of the cycle
- "Draws" - the number of draws
- "Cycle's numbers" - in the order they were drawn
4 - Key information: which cycle's numbers haven't been drawn yet
5 - Cycle's details (see below)
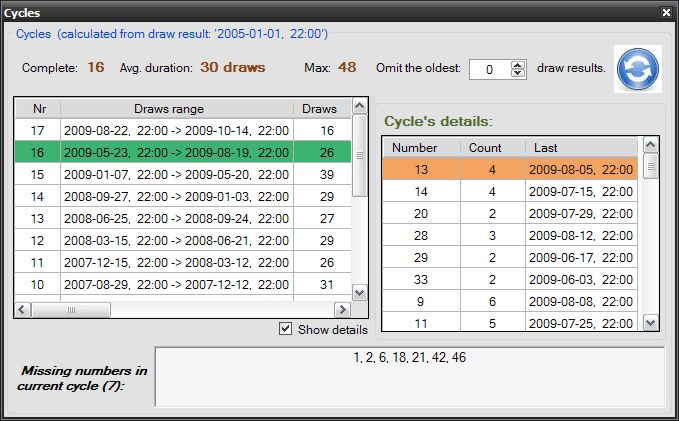
'Details' tell us about the behavior of the numbers during the cycle:
number of times each number was drawn, and the date it came up last..